3 سال پیش
زمان مطالعه : 20 دقیقه
بررسی میانگین متحرک وزن دار نمایی (Weighted Moving Average)
میانگین متحرک وزن دار نمایی چه به ما میگوید؟
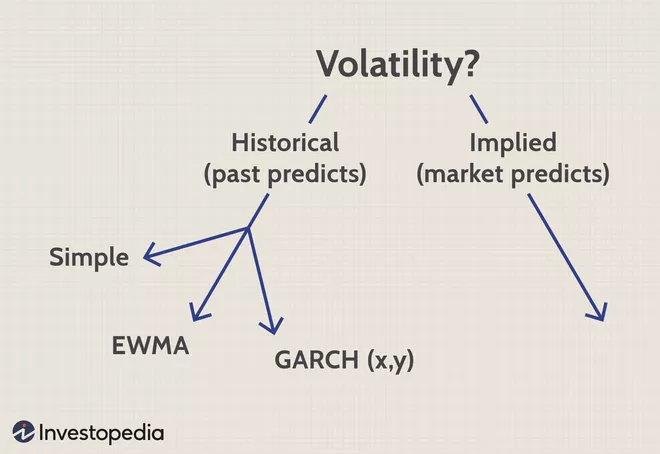
نوسانات تاریخی و ضمنی، دو رویکرد کلی نوسانات هستند. رویکرد تاریخی، گذشته سهام را به عنوان مرحله اولیه در نظر میگیرد. ما تاریخ را برای پیش بینی آینده سهام بررسی میکنیم. از سوی دیگر، نوسانات ضمنی (Implied volatility)، تاریخ را نادیده می گیرد و نوسانات ناشی از قیمت های بازار را پیدا می کند.

مقایسه نوسانات تاریخی با ضمنی
نوسانات تاریخی و ضمنی، دو رویکرد کلی نوسانات هستند. رویکرد تاریخی، گذشته سهام را به عنوان مرحله اولیه در نظر میگیرد. ما تاریخ را برای پیش بینی آینده سهام بررسی میکنیم. از سوی دیگر، نوسانات ضمنی (Implied volatility)، تاریخ را نادیده می گیرد و نوسانات ناشی از قیمت های بازار را پیدا می کند. طبق این رویکرد امیدواریم که بازار بهترین اطلاعات را داشته باشد و قیمت بازار، یک ارزیابی کلی از نوسان داشته باشد. در این مطلب به بررسی میانگین متحرک وزن دار نمایی میپردازیم.
با تمرکز بر سه رویکرد تاریخی (در سمت چپ بالا)، مشاهده میکنیم که آنها دو مرحله مشترک دارند، که عبارت اند از:
در این رابطه بخوانید : بلاک چین لایه 3 چیست و چگونه کار می کند؟
- مجموعه بازده های دوره ای را محاسبه کنید
- یک رویکرد وزن دار را اعمال کنید
ابتدا بازده دوره ای را محاسبه می کنیم. این بازده معمولاً مجموعهای از بازدههای روزانه است. در گزارش روزانه عادی، نسبت قیمت سهام را در نظر می گیریم (یعنی تقسیم قیمت امروز بر قیمت دیروز و غیره).

به صورت زیر:
Ui= بازده روز اول
Si==قیمت سهام در روز اول
Si-1==قیمت سهام یک روز قبلتر از روز اول
این فرمول یک سری بازده روزانه تولید می کند، از ui تا ui-m، و به تعداد روزهای اندازه گیری (m = روز) بستگی دارد.
این موضوع ما را به مرحله دوم می رساند: تفاوت این سه رویکرد در این مرحله است. در مقاله قبلی، نشان دادیم که طبق چند ساده سازی قابل قبول، واریانس ساده میانگین بازده مجذور است:

m= تعداد روز های محاسبه شده
n=روز اول
همچنین بخوانید : بناناگان (Banana Gun) چیست؟ و چگونه عمل میکند؟
u= تفاوت بازده با بازده میانگین
توجه کنید که این فرمول هر یک از بازده های دوره ای را جمع می کند، سپس کل آن را بر تعداد روزها یا مشاهدات (m) تقسیم می کند. بنابراین، در واقع فقط میانگینی از مجذور بازده دوره ای است. به عبارت دیگر به هر بازده مجذور، وزن مساوی داده می شود. بنابراین اگر آلفا (a) یک عامل وزنی باشد (به طور خاص، a = 1/m)، آنگاه یک واریانس ساده چیزی شبیه به این است:
میانگین متحرک وزن دار نمایی، در واریانس ساده بهبود می یابد
نقطه ضعف این رویکرد این است که همه بازده ها وزن یکسانی دارند. بازده دیروز، نسبت به بازده ماه گذشته تأثیر بیشتری بر واریانس ندارد. این مشکل با استفاده از میانگین متحرک وزندار نمایی (EWMA) که در آن بازدههای اخیر وزن بیشتری روی واریانس دارند، رفع میشود.
میانگین متحرک وزن دار نمایی (EWMA) لامبدا (lambda) را معرفی می کند که به آن پارامتر هموارسازی می گویند. لامبدا باید کمتر از یک باشد. در این شرایط، به جای وزنهای مساوی، هر بازده مجذور با یک ضریب به صورت زیر وزن میشود:
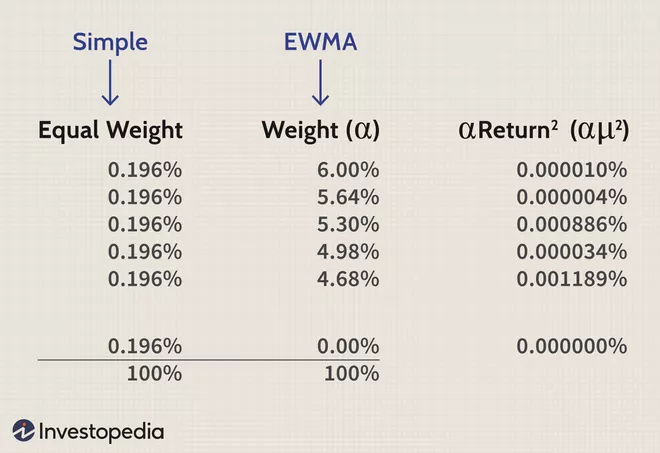
به عنوان مثال، سهام RiskMetricsTM، یک شرکت مدیریت ریسک مالی، تمایل دارد از لامبدا 0.94 یا 94٪ استفاده کند. در این مورد، اولین (جدیدترین) بازده دوره ای مجذور با (1-0.94) (.94) 0 = 6٪ وزن می شود. بازده مجذور بعدی صرفاً ضریب لامبدا وزن قبلی است. در این مورد 6٪ ضربدر 94٪ = 5.64٪. و وزن سومین روز قبل برابر است با (1-0.94) (0.94)2 = 5.30%.
این معنای “نمایی” در EWMA است: هر وزن یک ضریب ثابت (به عنوان مثال لامبدا، که باید کمتر از یک باشد) وزن روز قبل است. این امر واریانسی را تضمین می کند که نسبت به داده های جدیدتر وزن یا سوگیری دارد. تفاوت بین نوسانات ساده و EWMA برای Google در زیر نشان داده شده است.
نوسانات ساده به طور موثر هر بازده دوره ای را 0.196٪ وزن می کند، همانطور که در ستون O نشان داده شده است ( دو سال اطلاعات روزانه قیمت سهام شامل 509 بازده روزانه و 1/509 = 0.196٪). اما توجه داشته باشید که ستون P وزن 6٪، سپس 5.64٪، سپس 5.3٪ و غیره را اختصاص می دهد. این تنها تفاوت بین واریانس ساده و میانگین وزن دار نمایی است.
به یاد داشته باشید: پس از جمع کل مجموعه (در ستون Q) واریانس را بدست می آوریم که جذر انحراف استاندارد (standard deviation) است. اگر می خواهیم نوسان داشته باشیم، باید به خاطر داشته باشیم که جذر واریانس را بدست آوریم.
تفاوت نوسانات روزانه بین واریانس و میانگین وزن دار نمایی در مورد سهام گوگل چیست؟ قابل توجه است: واریانس ساده، نوسان روزانه 2.4% را بدست آورد اما میانگین وزن دار نمایی، نوسان روزانه 1.4% را بدست آورد. ظاهراً نوسانات گوگل، اخیراً کاهش یافته است. بنابراین، یک واریانس ساده ممکن است به طور ساختگی بالا باشد.
واریانس امروز تابعی از واریانس روز قبل است
ما باید مجموعه ای متوالی از وزنها را محاسبه کنیم که به طور تصاعدی کاهش مییابند. یکی از بهترین ویژگی های میانگین متحرک وزن دار نمایی این است که کل مجموعه به راحتی به یک فرمول تکرار شونده کاهش می یابد:

تکرار شونده به این معنی است که واریانس امروزی (یعنی تابعی از) واریانس روز قبل است. شما می توانید این فرمول را در جدول نیز بیابید، دقیقاً همان نتیجه محاسبه طولانی را ایجاد می کند! طبق این فرمول: واریانس امروز، برابر واریانس دیروز، به اضافه بازده مجذور دیروز است. توجه کنید که چگونه ما فقط دو عبارت را با هم جمع می کنیم: واریانس وزنی دیروز و بازده وزنی و مجذور دیروز.
با این حال، لامبدا پارامتر هموارسازی ما است. لامبدای بیشتر (به عنوان مثال، مانند 94٪ RiskMetric)، نشان دهنده افت آهسته قیمت مجموعه است. به صورت نسبی، ما نقاط داده بیشتری در مجموعه خواهیم داشت و آنها با سرعت بیشتری “ریزش” می کنند. از سوی دیگر، اگر لامبدا را کاهش دهیم، افت بیشتر را نشان میدهیم: وزنهها سریعتر سقوط میکنند و در نتیجه مستقیم افت سریع، نقاط داده کمتری استفاده میشود. (در صفحه گسترده، لامبدا یک ورودی است، بنابراین می توانید حساسیت آن را آزمایش کنید).
خلاصه مطلب
نوسان، انحراف استاندارد لحظه ای یک سهام و رایج ترین معیار ارزیابی ریسک است. نوسان، همچنین جذر واریانس است. ما می توانیم واریانس را به صورت تاریخی یا ضمنی (نوسانات ضمنی) اندازه گیری کنیم. هنگام اندازه گیری تاریخی، ساده ترین روش یک واریانس ساده است. اما نقطه ضعف واریانس ساده، یکسان بودن وزن همه بازده ها است. بنابراین ما با یک مبادله کلاسیک روبرو هستیم: ما همیشه دادههای بیشتری میخواهیم، اما هر چه دادههای بیشتری داشته باشیم، محاسبات ما با دادههای دور (غیر مرتبط) کاهش مییابد. میانگین متحرک وزنی نمایی (EWMA) با تخصیص وزن به بازده های دوره ای، واریانس ساده را بهبود می بخشد. با انجام این کار، هم میتوانیم از حجم نمونه بزرگ استفاده کنیم، هم میتوانیم به بازدههای اخیر وزن بیشتری بدهیم.
ترجمه شده توسط مجله خبری نیپوتو
در نیپوتو مارکت امکان خرید و فروش بایننس کوین برای شما فراهم شده است.
خرید و فروش ارزهای دیجیتال از امروز شروع کنید
ممکن است علاقه مند باشید
ثبت دیدگاه
لیست نظرات (0)
انتخاب سردبیر
مفاهیم پایه
بیشتر بخوانید